vector and matrix norms
>> norm(X, p) x for matrix, p for p-norm (default is 2)
determinate, inverse and pseudoinverses
>>det(D) D for matrix for determinate (行列式)
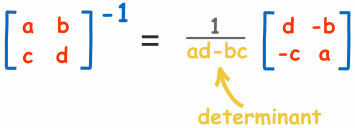
For a 2×2 matrix (2 rows and 2 columns):

The determinant is:
|A| = ad - bc
"The determinant of A equals a times d minus b times c"
"The determinant of A equals a times d minus b times c"
>>pinv(E) E for matrix for pseudoinverse
Matrix powers and exponentials
>>F^2 F for matrix
>>F.^2 F for matrix
>>sqrt(F) F for matrix
Eigenvalue and eigenVectors
>>eig(g) G for matrix
We can rewrite the condition Av=  v as v as(A−  I)v=0 I)v=0 where I is the n  n identity matrix. Now, in order for a non-zero vector v to satisfy this n identity matrix. Now, in order for a non-zero vector v to satisfy this equation, A−  I must not be invertible. I must not be invertible. |
|
 I must equal 0. We call p(
I must equal 0. We call p( )=det(A−
)=det(A− I) the characteristic polynomial of A. The eigenvalues of A are simply the roots of the characteristic polynomial of A.
I) the characteristic polynomial of A. The eigenvalues of A are simply the roots of the characteristic polynomial of A.Data analysis
>>min(Data)
>>max(Data)
>>std(Data)
his is the formu
la for Standard Deviation:

>>cov(Data)
>>corrcoef(Data)

>>cov(Data)
>>corrcoef(Data)